What do we do when we think that a particular set of effects is likely to vary significantly across groups? There seem to be two basic approaches: we can either (a) run separate models for each group or we can (b) pool data across groups and then allow effects to vary through the inclusion of interaction terms (i.e. run a fully-interacted model). In terms of coefficients, the two approaches will ultimately produce equivalent results.* The standard errors, however, are a different story. This inevitably has implications for things like statistical significance, a subject with which sociologists in particular are known to be preoccupied.

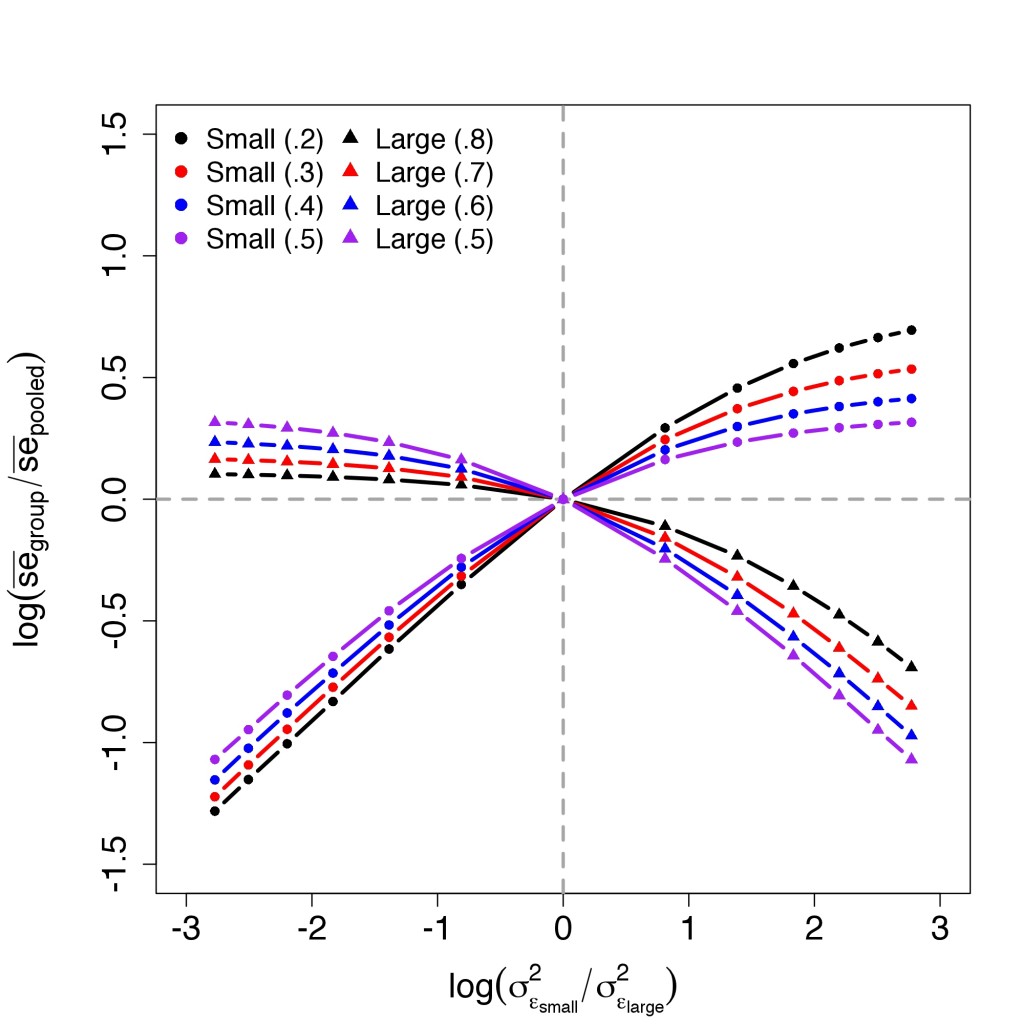
A common intuition is that these changes are due to changes in the degrees of freedom resulting from disaggregation. Having recently run into this suggestion in a couple of different places, I decided to make up some data to get a better sense of how standard errors are affected by groupwise disaggregation (i.e. running separate models for each group as opposed to running a single pooled model with a bunch of interaction effects). I was interested in particular in the way which the expansion and contraction of group-specific standard errors varies depending on differences in group size and error variance. The results of this experiment are shown in the graph below which, in effect, depicts the expansion and contraction of standard errors as a function of the level of groupwise heteroscedasticity. To anticipate the discussion below the break, the main finding here seems to be that, on average, disaggregation has no effect on standard errors in the absence of heteroscedasticity.**

Values along the -axis represent the average degree of change in the size of the standard error of a bivariate regression coefficient resulting from disaggregation, with change measured in terms of the log of the ratio of the group-specific standard error to the corresponding standard error in the pooled model. Averages are calculated across 1000 randomly-generated sets of data, each of which was composed of a small group and a large group, with group size defined as a fraction of the total sample size. In addition to allowing the size of the groups to vary, I also allowed the degree of groupwise heteroscedasticity to vary. This is reflected in variation along the the -axis which depicts the log of the ratio of error variances between the small and large group.

Whereas values along the -axis are estimated from the data, values along the -axis are a function of the input used in the data generating function shown below:

simdat<-function(n, sigmasq){
  b<-runif(1,-.5,.5)
  x<-rnorm(n, runif(1,1,5))
  y<-x*b + rnorm(n, sd = sqrt(sigmasq))
  dat<-data.frame(y,x)
  dat
}

This function is designed to produce a dataset consisting of a single predictor variable x and a single outcome y. Values of x are determined by random draws from a normal distribution with a mean of 0 and a randomly chosen standard deviation which varies uniformly between 1 and 5. Values of y are defined as a combination of a systematic component given by x*b and a random component determined by a random draw from a normal distribution with a mean 0 and a standard deviation of sqrt(sigmasq). Values of b are drawn at random from a uniform distribution varying between -0.5 and 0.5. In this context, b defines the "true" value of the regression coefficient associated with the regression of y on x, while sigmasq defines the "true" variance of the corresponding error term. The size of the resulting data set is determined by the value of n which, along with sigmasq, is set by the user. For the purposes of this exercise, n was set to 1000 while sigmasq was set to 9 which implies that errors are drawn from a normal distribution with a mean of 0 and a standard deviation of 3.

By manipulating the values of n and sigmasq, we can create data sets of varying sizes with varying degrees of variance in the pooled errors. By combining data sets produced in this manner, we can also create pooled data sets which vary in terms of the relative size of its constituent groups, as well as in terms of the level of groupwise heteroscedasticity. Data generation and model comparison are carried out using the follow which draws on the simdat function described above:

simreg<-function(frac, n = 1000, sigmasq = 9, xf = 1){
  gsize<-round(frac*n)
  large<-cbind(simdat(n - gsize, sigmasq),z = factor(0))
  small<-cbind(simdat(gsize, sigmasq*xf), z = factor(1))
  pool<-rbind(large, small)
  large.model<-lm(y~x, data = large)
  small.model<-lm(y~x, data = small)
  pool.model<-lm(y~0+z+x:z, data = pool)  
  large.se<-coef(summary(large.model))[2,2]
  small.se<-coef(summary(small.model))[2,2]
  large.ratio<-large.se/coef(summary(pool.model))[3,2]
  small.ratio<-small.se/coef(summary(pool.model))[4,2]
  results<-cbind(small = log(small.ratio), large = log(large.ratio))
  results
}

This function generates data for both a large group and a small group. These are then combined to create a pooled dataset. The function then runs separate models for each set of data, returning (a) the log of the ratio of the standard error from the large group model to the standard error from the pooled model, and (b) log of the ratio of the standard error from the small group model to the standard error from the pooled model. The degree of groupwise heteroscedasticity is defined by the value of xf which is used to set the size of error variance of the large group (sigmasq*xf) relative to the size of the error variance of the small group (sigmasq).

The simreg function was executed 1000 times for each combination of sample sizes and error variances shown in the graph above. The results clearly indicate that when the error variance of the small group is larger than that of the big group, groupwise disaggregation will, on average, lead to an increase in the standard errors of the small group and a decrease in the standard errors of the big group. The opposite holds when the error variance of the small group is less than that of the big group. The magnitude of these changes is a function of the relative size of each group. More specifically, as group size becomes increasingly unbalanced, the standard errors of the large group are increasingly unaffected by disaggregation. The opposite holds for the small group.

This makes perfect sense if we think about the error variance in the pooled model as the weighted average of group-specific error variances, with weights defined in terms of a group's share of the pooled degrees of freedom. When group size is extremely unbalanced, the pooled error variance is going to be pulled towards the error variance of the larger group. As such, the standard error associated with the large group isn't going to change much as a result of disaggregation. In contrast, the standard error associated with the small group will appear to move a lot as a result of its dissimilarity to the pooled variance. When groups are perfectly balanced, the degree of movement in the standard errors is going to be determined exclusively by the degree of groupwise heteroscedasticity.

We can obviously work all of this out formally as well. That is, in this context, simulation isn't going to show us something we couldn't understand otherwise. Sometimes it is simply easier to use the brute force of simulation than it is to work through the formulas. The results are often more intuitive in the sense that they take the form of a concrete experiment. This is one of the reasons why simulation is such a useful teaching tool. Among other things, it can be used illustrate topics such long-run probability or the idea of a sampling distribution.

* If the pooled model is parameterized in the usual way (i.e. in terms of differences with respect to a reference group), the group-specific coefficients and standard errors associated with each of the non-reference categories are calculated separately from the model itself. This is, of course, what we are doing when we look at a table of coefficients and mentally add the effect of a two-way interaction to the effect of one of its constituent terms. Things are obviously a bit more difficult in the case of standard errors.

** Note that the discussion here is about standard errors and not significance. The latter issue gets a little more complicated when we use methods such as a -test which refers to a distribution whose shape varies with the degrees of freedom. My hunch is that so long as the smallest group in the data has a reasonable number of observations, this shouldn't matter too much in practice, even if the resulting -values vary between the pooled and group-specific models.